Getting acquainted with different regression models using scientific data from different sources

Friday. November 02, 2018 - 41 mins

Subset selection, regularization

1, Forward stepwise selection

(-), Download data from http://science.sciencemag.org/content/early/2018/01/17/science.aar3247 (has been a previous hw)
(-), Load protein levels, and convert them to numerical values if necessary (has been a previous hw)
(-), Inspect missing values, and drop patients with missing values in protein levels (has been a previous hw)
(-), Load cancer labels (has been a previous hw)

%pylab inline
import pandas as pd
from sklearn import metrics as ms
from sklearn.preprocessing import normalize
from sklearn.model_selection import train_test_split
import statsmodels.tools as smt

Populating the interactive namespace from numpy and matplotlib

# modified excel file - header names deleted
xls = pd.ExcelFile('aar3247_Cohen_SM_Tables-S1-S11.xlsx')
# protein levels
protein_levels = pd.read_excel(xls, 'Table S6')
cancerTypes = pd.read_excel(xls, 'Table S11')

tumorTypeAndProteinLevels = np.array(['Tumor type','AFP (pg/ml)',
        'Angiopoietin-2 (pg/ml)', 'AXL (pg/ml)', 'CA-125 (U/ml)',
        'CA 15-3 (U/ml)', 'CA19-9 (U/ml)', 'CD44 (ng/ml)','CEA (pg/ml)',
        'CYFRA 21-1 (pg/ml)', 'DKK1 (ng/ml)', 'Endoglin (pg/ml)',
        'FGF2 (pg/ml)', 'Follistatin (pg/ml)', 'Galectin-3 (ng/ml)',
        'G-CSF (pg/ml)', 'GDF15 (ng/ml)', 'HE4 (pg/ml)', 'HGF (pg/ml)',
        'IL-6 (pg/ml)', 'IL-8 (pg/ml)', 'Kallikrein-6 (pg/ml)',
        'Leptin (pg/ml)', 'Mesothelin (ng/ml)', 'Midkine (pg/ml)', 
        'Myeloperoxidase (ng/ml)', 'NSE (ng/ml)', 'OPG (ng/ml)', 
        'OPN (pg/ml)', 'PAR (pg/ml)', 'Prolactin (pg/ml)',
        'sEGFR (pg/ml)', 'sFas (pg/ml)', 'SHBG (nM)',
        'sHER2/sEGFR2/sErbB2 (pg/ml)', 'sPECAM-1 (pg/ml)',
        'TGFa (pg/ml)', 'Thrombospondin-2 (pg/ml)', 'TIMP-1 (pg/ml)',
        'TIMP-2 (pg/ml)'])

# Remove * and ** values
plvls = protein_levels[tumorTypeAndProteinLevels].applymap(
    lambda x: float(x[2:]) if type(x)==str and x[0:2]=="**" else x)
plvls = plvls.applymap(
    lambda x: float(x[1:]) if type(x)==str and x[0:1]=="*" else x)

# Drop rows containing NaN or missing value
plvls = plvls.dropna(axis='rows')

# Extract cancer types for all the corresponding protein levels
cancer_types = np.array(list(map(lambda x: 1 if x=="Normal" else 0,
                                 plvls['Tumor type'].values)))
plvls = plvls[tumorTypeAndProteinLevels[1:]]

# Normalize
plvls = pd.DataFrame(normalize(plvls, axis=1),
                     columns=tumorTypeAndProteinLevels[1:])

(A), Perform forward iterative subset selection using statsmodels logistic regression when predicting the cancer/normal binary labels using protein levels as inputs. Use the log-likelihood values to select the best additional variable in each iteration.

from statsmodels.discrete.discrete_model import LogitResults, Logit

def iteratively_select_variables(data, data_labels, max_variables=3):
    max_variables = max_variables if data.columns.size > 3 else data.columns.size//2
    # Labels 
    labels = data.columns
    # Best labels
    best_labels = []
    best_log_losses = []
    best_aics = []
    best_bics = []
    for var in range(max_variables):
        log_losses = []
        aics = []
        bics = []
        for label in labels:
            # Logistic model on binary cancer -> healthy or not
            model = Logit(data_labels, smt.add_constant(data[np.append(best_labels, label)]))
            # basinhopping seems to be the best option
            result = model.fit(method='basinhopping', full_output=True, disp=False)
            log_losses.append(-model.loglike(result.params))
            aics.append(result.aic)
            bics.append(result.bic)
        # Find the min loss fit
        min_loss_ind = np.argmin(log_losses)
        # Update the output values
        best_log_losses.append(log_losses[min_loss_ind])
        best_aics.append(aics[min_loss_ind])
        best_bics.append(bics[min_loss_ind])
        # Update best labels and labels
        best_labels = np.append(best_labels, labels[min_loss_ind])
        labels = np.delete(labels, [min_loss_ind])
    return best_labels, best_log_losses, best_aics, best_bics

labels, losses, aics, bics = iteratively_select_variables(plvls, cancer_types, max_variables=6)

2, Subset selection

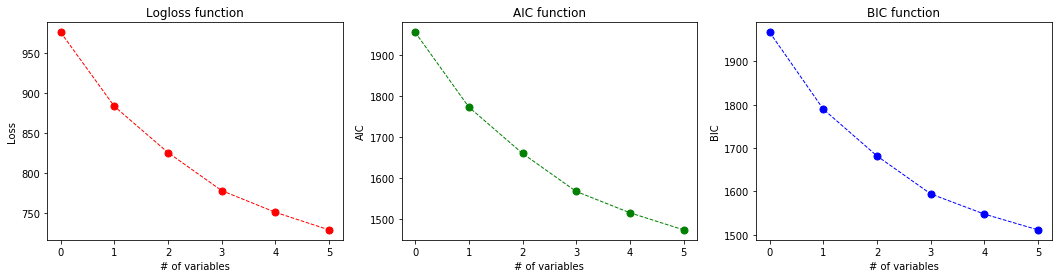
(A), Plot the AIC and the BIC criterion values depending on the number of variables during forward subset selection. Interpret the result based on the formulas for the 2 criteria!

import itertools

def findsubsets(S,m):
    return set(itertools.combinations(S, m))

def plot_output_curves(labels, losses, aics, bics):
    plt.figure(figsize=(18, 4))
    # Loss function
    plt.subplot("131")
    plt.plot(range(len(labels)), losses, 'ro--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('Loss')
    plt.xticks(range(len(labels)))
    plt.title("Logloss function")
    # AIC function
    plt.subplot("132")
    plt.plot(range(len(labels)), aics, 'go--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('AIC')
    plt.xticks(range(len(labels)))
    plt.title("AIC function")
    # BIC function
    plt.subplot("133")
    plt.plot(range(len(labels)), bics, 'bo--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('BIC')
    plt.xticks(range(len(labels)))
    plt.title("BIC function")

plot_output_curves(labels, losses, aics, bics)

png

def plot_aic_bic_difference(aics, bics):
    plt.figure(figsize=(8, 4))
    # AIC function
    plt.plot(range(len(labels)), aics, 'go--', linewidth=1, markersize=7, label='AIC')
    plt.xlabel('# of variables')
    plt.xticks(range(1, len(labels)+1))
    # BIC function
    plt.plot(range(len(labels)), bics, 'bo--', linewidth=1, markersize=7, label='BIC')
    plt.xlabel('# of variables')
    plt.ylabel('AIC/BIC values')
    plt.title("AIC/BIC functions")
    plt.legend()
    plt.show()

plot_aic_bic_difference(aics, bics)

png

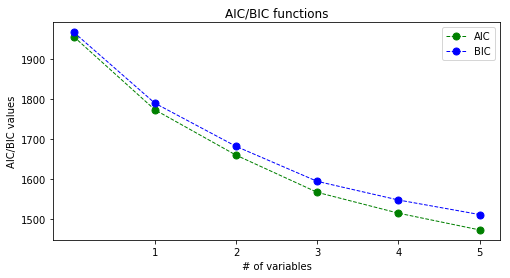
Tha BIC curve is constantly above the AIC curve but the trend seems to be the same. It is due to the fact that the calculation of the two constants is almost the same, but BIC is proportional to log(n)/n while AIC is to 2/n thus AIC is decreasing faster with the increase in n.

(B), Plot the AUC from a 5-fold cross validation (use sklearn KFold with random_state=0), depending on the number of variables during forward model selection. What do you see compared to the curves from AIC, and BIC?

def iteratively_select_variables_with_cross_validation(data, data_labels, max_variables=3):
    max_variables = max_variables if data.columns.size > 3 else data.columns.size//2
    # Labels 
    labels = data.columns
    # Best labels
    best_labels = []
    best_log_losses = []
    best_aics = []
    best_bics = []
    best_aucs = []
    for var in range(max_variables):
        log_losses = []
        aics = []
        bics = []
        aucs = []
        for label in labels:
            cross_losses = []
            cross_aics = []
            cross_bics = []
            cross_aucs = []
            # 5 fold cross validate
            for k in range(5):
                X_train, X_test, y_train, y_test = train_test_split(
                    smt.add_constant(data[np.append(best_labels, label)]), cancer_types,
                    test_size=0.20, random_state=0)
                # Logistic model on binary cancer -> healthy or not
                model = Logit(y_train, X_train)
                # basinhopping seems to be the best option
                result = model.fit(method='basinhopping', full_output=True, disp=False)
                y_pred = result.predict(X_test)
                fpr, tpr, _ = ms.roc_curve(y_test, y_pred)
                cross_losses.append(-model.loglike(result.params))
                cross_aics.append(result.aic)
                cross_bics.append(result.bic)
                cross_aucs.append(ms.auc(fpr, tpr))
            log_losses.append(np.mean(cross_losses))
            aics.append(np.mean(cross_aics))
            bics.append(np.mean(cross_bics))
            aucs.append(np.mean(cross_aucs))
        # Find the min loss fit
        min_loss_ind = np.argmin(log_losses)
        # Update the output values
        best_log_losses.append(log_losses[min_loss_ind])
        best_aics.append(aics[min_loss_ind])
        best_bics.append(bics[min_loss_ind])
        best_aucs.append(aucs[min_loss_ind])
        # Update best labels and labels
        best_labels = np.append(best_labels, labels[min_loss_ind])
        labels = np.delete(labels, [min_loss_ind])
    return best_labels, best_log_losses, best_aics, best_bics, best_aucs

labels, losses, aics, bics, aucs = iteratively_select_variables_with_cross_validation(plvls, cancer_types)

def plot_aic_bic_auc_curves(labels, aics, bics, aucs):
    plt.figure(figsize=(16, 4))
    # AIC function
    plt.subplot("131")
    plt.plot(range(len(labels)), aics, 'ro--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('AIC')
    plt.xticks(range(len(labels)))
    plt.title("AIC function")
    # AIC function
    plt.subplot("132")
    plt.plot(range(len(labels)), bics, 'go--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('BIC')
    plt.xticks(range(len(labels)))
    plt.title("BIC function")
    # BIC function
    plt.subplot("133")
    plt.plot(range(len(labels)), aucs, 'bo--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('AUC')
    plt.xticks(range(len(labels)))
    plt.title("AUC function")

plot_aic_bic_auc_curves(labels, aics, bics, aucs)

png

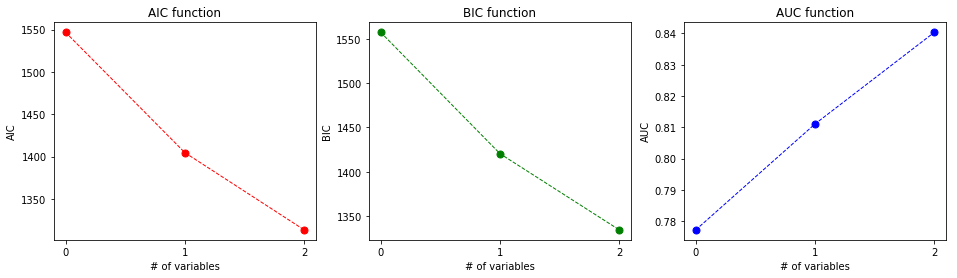
The area under the curve (AUC) gets higher and higher with adding variables. Using only one cross validation for the best labels:

def cross_validate_with_labels(labels, data, data_labels):
    cross_losses = []
    cross_aics = []
    cross_bics = []
    cross_aucs = []
    # 5 fold cross validate
    for k in range(5):
        X_train, X_test, y_train, y_test = train_test_split(
                    smt.add_constant(data[labels]), data_labels,
                    test_size=0.20, random_state=0)
        # Logistic model on binary cancer -> healthy or not
        model = Logit(y_train, X_train)
        # basinhopping seems to be the best option
        result = model.fit(method='basinhopping', full_output=True, disp=False)
        y_pred = result.predict(X_test)
        fpr, tpr, _ = ms.roc_curve(y_test, y_pred)
        cross_losses.append(-model.loglike(result.params))
        cross_aics.append(result.aic)
        cross_bics.append(result.bic)
        cross_aucs.append(ms.auc(fpr, tpr))
    return cross_losses, cross_aics, cross_bics, cross_aucs

def plot_cross_validated_data(labels, data, data_labels):
    loss, aics, bics, aucs = cross_validate_with_labels(labels, data, data_labels)
    plt.figure(figsize=(10, 10))
    x = range(5)
    # Loss function
    plt.subplot("221")
    plt.plot(x, loss, 'ro--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('Loss')
    plt.xticks(x)
    plt.title("Loss function")
    # AIC function
    plt.subplot("222")
    plt.plot(x, aics, 'ro--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('AIC')
    plt.xticks(x)
    plt.title("AIC function")
    # BIC function
    plt.subplot("223")
    plt.plot(x, bics, 'go--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('BIC')
    plt.xticks(x)
    plt.title("BIC function")
    # AUC function
    plt.subplot("224")
    plt.plot(x, aucs, 'bo--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('AUC')
    plt.xticks(x)
    plt.title("AUC function")

plot_cross_validated_data(labels, plvls, cancer_types)

png

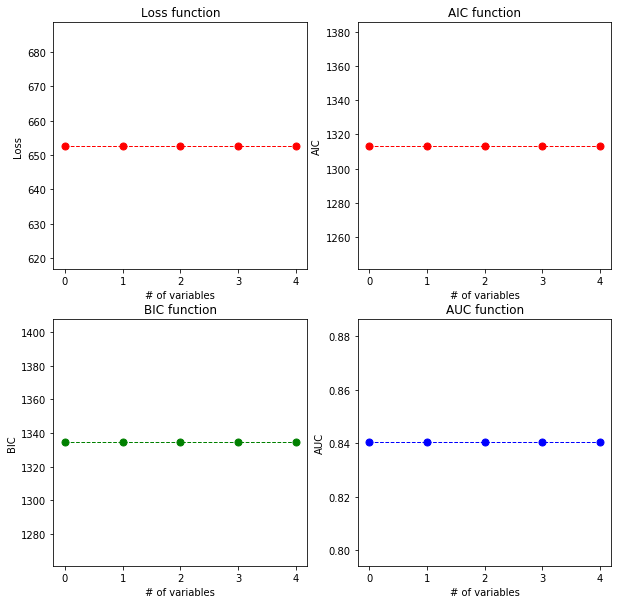
3, Comparison of tools

(-), Estimate the AUC of a fit with 5-fold cross validation (use sklearn KFold with random_state=0) using the logistic regression from statsmodels using all variables. (has been a previous hw)
(-), Repeat it with logistic regression fom sklearn. (has been a previous hw)
(A), Sci-kit learn will be less accurate than statsmodels in this dataset. What are the resons behind the difference?
(B), Try to fix the problems, and produce a fit witk sklearn which has a 5-fold CV AUC very close (diff<0.0001) to the one with statmodels.

# Cross validate
def cross_validate(plvls, cancer_types, k_fold=5):
    logloss = []
    accuracy = []
    fpr = dict()
    tpr = dict()
    auc = []
    for i in range(k_fold):
        # Splitting the randomized data 20%-80%
        X_train, X_test, y_train, y_test = train_test_split(smt.add_constant(plvls), cancer_types,
                                                            test_size=1./k_fold,
                                                            random_state=137*i + i*42, shuffle=True)

        # Logistic model on binary cancer -> healthy or not
        logistic_model = Logit(y_train, X_train)
        # basinhopping seems to be the best option
        results = logistic_model.fit(method='basinhopping', full_output=True, disp=False)

        # logloss is the negative loglike function
        logloss.append(-logistic_model.loglike(results.params))

        train_prediction = results.predict(X_test)
        pred = train_prediction
        truth = y_test

        accuracy.append(100.*ms.accuracy_score(truth, np.array(list(map(lambda x: 1 if x > 0.5 else 0, train_prediction)))))

        fpr[i], tpr[i], threshold = ms.roc_curve(truth, pred)
        
        auc.append(ms.auc(fpr[i], tpr[i]))
        
    return logloss, accuracy, auc, fpr, tpr

def plot_cross_validated_data(values, k_fold=5):
    
    logloss, accuracy, auc, fpr, tpr = values
    
    print("Mean Accuracy = %.4f%%" % np.mean(accuracy))
    if(len(logloss) > 0):
        print("\t\t Mean logloss = %.3f" % np.mean(logloss))
    
    plt.figure(figsize=(8.,8.))
    lw = 2
    cmap = ['r', 'g', 'b', 'c', 'darkorange']
    for i in range(k_fold):
        plt.plot(fpr[i], tpr[i], color=cmap[i%5],lw=lw, linestyle='--', label="AUC = %.3f " % auc[i])
    plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='-', label="Mean AUC = %.3f +/- %.3f" %
             (np.mean(auc), np.std(auc)))
    plt.xlim([0.0, 1.0])
    plt.ylim([0.0, 1.0])
    plt.xlabel('False Positive Rate')
    plt.ylabel('True Positive Rate')
    plt.legend(loc="lower right")
    plt.show()

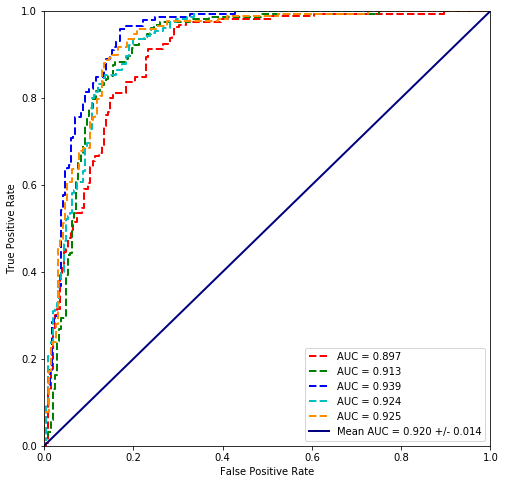
plot_cross_validated_data(cross_validate(plvls.values, cancer_types))

Mean Accuracy = 85.0970%
		 Mean logloss = 475.912

png

from sklearn.metrics import log_loss

# Cross validate
def scikit_cross_validate(model, plvls, cancer_types, k_fold=5):
    logloss = []
    accuracy = []
    mse = []
    fpr = dict()
    tpr = dict()
    auc = []
    for i in range(k_fold):
        # Splitting the randomized data 20%-80%
        X_train, X_test, y_train, y_test = train_test_split(smt.add_constant(plvls), cancer_types,
                                                            test_size=1./k_fold,
                                                            random_state=137*i + i*42, shuffle=True)

        # Logistic model on binary cancer -> healthy or not
        clf = model.fit(X_train, y_train)

        train_prediction = clf.predict(X_test)
        pred_value = clf.decision_function(X_test)
        pred_proba = clf.predict_proba(X_test)
        pred = train_prediction
        truth = y_test

        logloss.append(log_loss(truth, pred_proba))
        
        accuracy.append(100.*ms.accuracy_score(truth, train_prediction))

        fpr[i], tpr[i], threshold = ms.roc_curve(truth,  pred_value)
        
        auc.append(ms.auc(fpr[i], tpr[i]))
        
    return logloss, accuracy, auc, fpr, tpr

from sklearn.linear_model import LogisticRegression
plot_cross_validated_data(scikit_cross_validate(LogisticRegression(penalty='l1', C=156), 
                                                plvls.values, cancer_types))

Mean Accuracy = 85.0970%
		 Mean logloss = 0.356

png

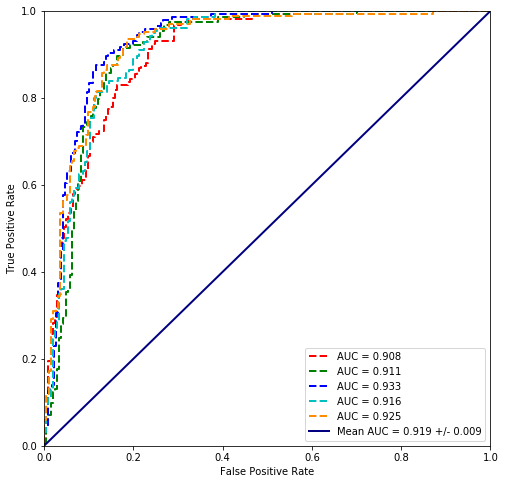
It seems that the scikit regression performs worse which might be do to regularization, which is also possible wih statsmodels. However I am not doing it by using regularized fit via statmodels but trying to disable regularization of the sklearn package. It is not actually possible but setting the C parameter large enough (156) it is possible to calculate them with the same accuracy. reference

4, Large dimensional regression

Load the prepared data file “methyl.csv” (Which is a subset of the data from the article: https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3780611/ )
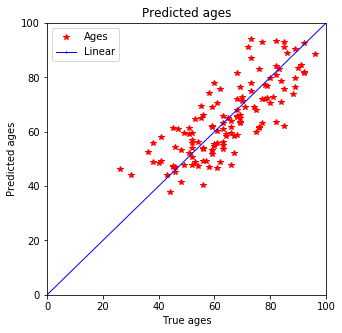
(A), Predict the age of people based on methylation values, using linear regression with a 80-20% train-test split (use sklearn train-test split with random_state=0). Plot the scatterplot of true values vs predictions for both the training and the testing set, what do you see?

methyl = pd.read_csv("small_met.csv", sep='\t')
methyl_values = methyl.values[:, 1:methyl.columns.size-1]
ages = methyl['age'].values

from sklearn.linear_model import LinearRegression
X_train, X_test, y_train, y_test = train_test_split(methyl_values, ages, shuffle=True, random_state=0)
clf = LinearRegression().fit(X_train, y_train)
pred_train = clf.predict(X_train)
pred_test = clf.predict(X_test)

def plot_predictions(y_true, y_pred):
    plt.figure(figsize=(5, 5))
    plt.plot(y_true, y_pred, 'r*', markersize=6, label='Ages')
    plt.title("Predicted ages")
    plt.xlabel("True ages")
    plt.ylabel("Predicted ages")
    plt.plot(np.linspace(0, 101, 2), np.linspace(0, 101, 2), 'bo-', markersize=1, linewidth=1, label='Linear')
    plt.xlim(0, 100)
    plt.ylim(0, 100)
    plt.legend()
    plt.show()

Predictions for the training data

plot_predictions(y_train, pred_train)

png

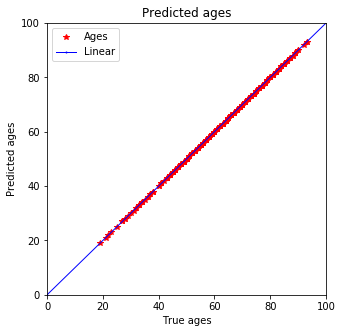
Well, it is not so linear…

plot_predictions(y_test, pred_test)

png

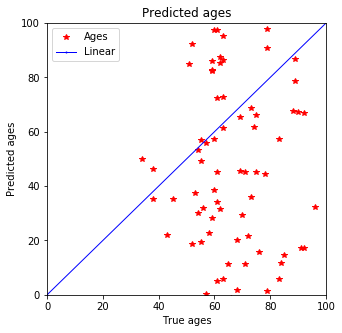
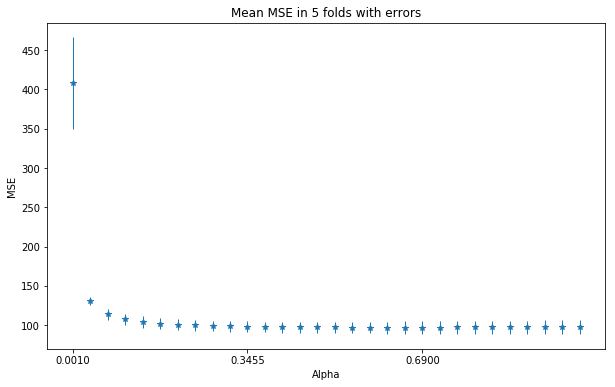
(B), Plot the MSE with 5 fold CV, using Ridge regression, depending on the penalty threshold. Find and optimal penalty value.
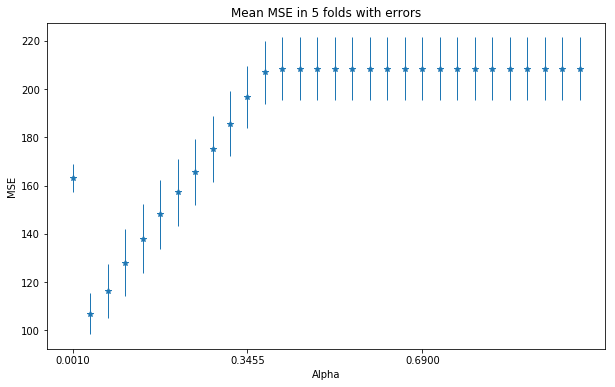
(C), Plot the MSE with 5 fold CV, using lasso regression, depending on the penalty threshold. Find and optimal penalty value. Inspect how many coefficients are 0?
(D), Use the best model found by the methods above to predict age from methylation with a 80-20% train-test split (use sklearn train-test split with random_state=0). Plot the scatterplot of true values vs predictions for both the training and the testing set.

from sklearn.linear_model import Ridge
from sklearn.metrics import log_loss, mean_squared_error

# Cross validate
def scikit_cross_validate(model, data, data_labels, k_fold=5):
    logloss = []
    accuracy = []
    mse = []
    fpr = dict()
    tpr = dict()
    auc = []
    for i in range(k_fold):
        # Splitting the randomized data 20%-80%
        X_train, X_test, y_train, y_test = train_test_split(smt.add_constant(data), data_labels,
                                                            test_size=1./k_fold,
                                                            random_state=137*i + i*42, shuffle=True)

        # Logistic model on binary cancer -> healthy or not
        clf = model.fit(X_train, y_train)

        train_prediction = clf.predict(X_test)
        pred = train_prediction
        truth = y_test
        
        mse.append(mean_squared_error(truth, pred))
        
    return mse, clf.coef_

def plot_mse_in_ridge_alpha_range(model, data, data_labels, ran=np.linspace(0.001, 1, 30), k_fold=5):
    i = 1
    mses = []
    std_mses = []
    coefs = []
    for val in ran:
        mse, coef = scikit_cross_validate(model(alpha=val), data, data_labels, k_fold=k_fold)
        mses.append(np.mean(mse))
        std_mses.append(np.std(mse))
        coefs.append(coef)
    plt.figure(figsize=(10,6))
    plt.errorbar(ran, mses, yerr=std_mses, fmt='*', elinewidth=1)
    plt.xlabel('Alpha')
    plt.ylabel('MSE')
    plt.xticks(ran[::10])
    plt.title("Mean MSE in 5 folds with errors")
    plt.show()

np.set_printoptions(precision=3)
plot_mse_in_ridge_alpha_range(Ridge, methyl_values, ages)

png

from sklearn.linear_model import Lasso
plot_mse_in_ridge_alpha_range(Lasso, methyl_values, ages)

png

(D), Use the best model found by the methods above to predict age from methylation with a 80-20% train-test split (use sklearn train-test split with random_state=0). Plot the scatterplot of true values vs predictions for both the training and the testing set.

Seeing the examples above the Ridge regression is the candidate for sure. The regression seesm stable from 0.35 thus I’ll set the alpha to be sure to .69

X_train, X_test, y_train, y_test = train_test_split(methyl_values, ages, shuffle=True, random_state=0)
clf = Ridge(alpha=0.69).fit(X_train, y_train)
pred_train = clf.predict(X_train)
pred_test = clf.predict(X_test)

Training prediction

plot_predictions(y_train, pred_train)

png

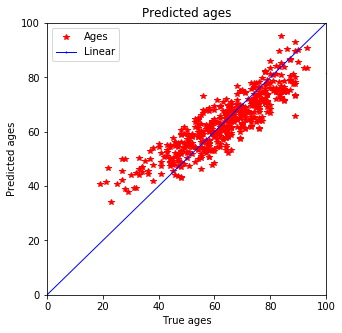
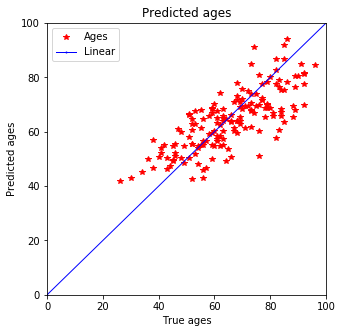
Test prediction - actually seems much better as before

plot_predictions(y_test, pred_test)

png

5, Shrinkage and coefficient selection

(A), Show on one plot each coefficient with a line using Ridge regression, depending on the penalty threshold.
(B), Show on one plot each coefficient with a line using Lasso regression, depending on the penalty threshold.

def plot_coefs(model, data, data_labels, ran=np.linspace(0.1, 4, 35), k_fold=5):
    coefs = []
    for ind, val in enumerate(ran):
        _, coef = scikit_cross_validate(model(alpha=val), data, data_labels, k_fold=k_fold)
        coefs.append(coef)
    coefs = np.array(coefs).T
    plt.figure(figsize=(12, 12))
    for ind, line in enumerate(coefs):
        plt.plot(ran, line, 'r--', markersize=3, linewidth=1)
    plt.xlabel('alhpa')
    plt.ylabel('coefficient')
    plt.title('Regression coeffiecent distro by alpha parameter')
    plt.show()

Ridge regression coefficients

plot_coefs(Ridge, methyl_values, ages)

png

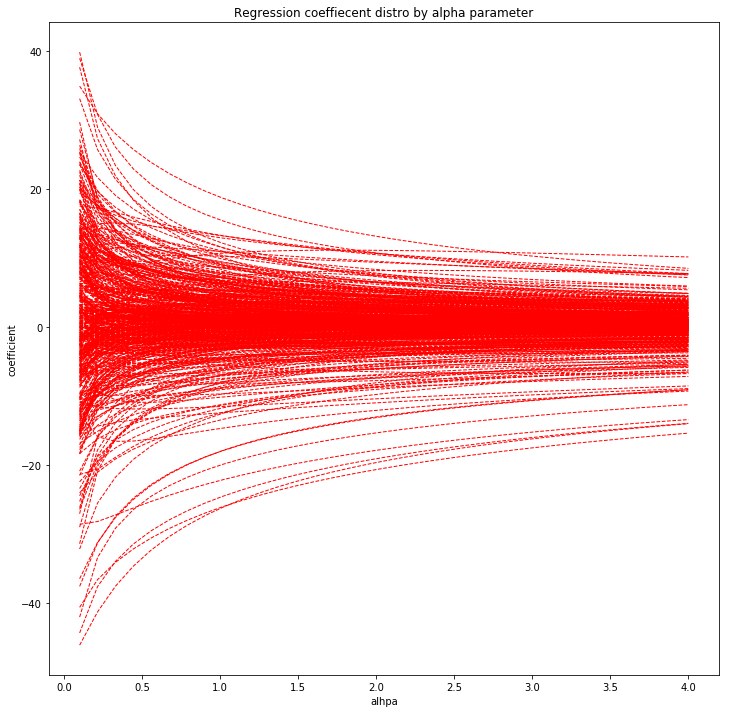
Lasso regression coefficients

plot_coefs(Lasso, methyl_values, ages, ran=np.linspace(0.0015,0.25,35))

png

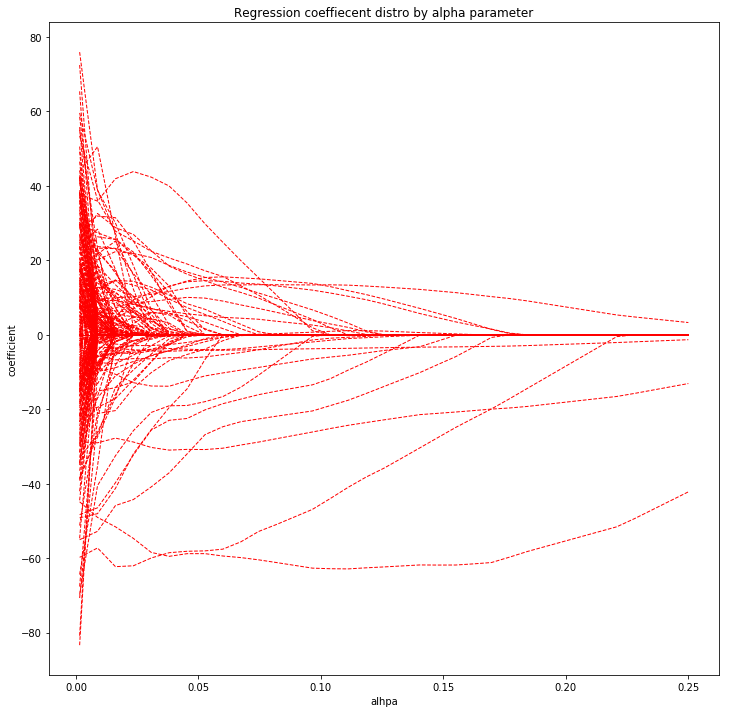
(C), Reuse your code form 1,2 and: Perform forward iterative subset selection with linear regression (use sklearn its much faster). Use the R-squared values to select the best additional variable in each iteration. Plot the AIC and the BIC values and MAE from 5-fold cross validation (use sklearn KFold with random_state=0) depending on the number of variables during forward model selection. Which is the best number of variables? This will take quite some time, at least go up to 150 variables selected.
(D), Use the best linear regression model found by forward subset selection to predict age from methylation with a 80-20% train-test split (use sklearn train-test split with random_state=0). Plot the scatterplot of true values vs predictions for both the training and the testing set. How does it look compared to 4/(D)?

from statsmodels.regression.linear_model import OLS

def scikit_iteratively_select_variables_with_cross_validation(data, data_labels, max_variables=3):
    max_variables = max_variables if data.columns.size > 3 else data.columns.size//2
    # Labels 
    labels = data.columns
    # Best labels
    best_labels = np.array([])
    best_r_squared = []
    best_aics = []
    best_bics = []
    best_maes = []
    for var in range(max_variables):
        print('Variables: ', var+1, end='\t')
        r_squared = []
        aics = []
        bics = []
        maes = []
        for label in labels:
            cross_r_squared = []
            cross_aics = []
            cross_bics = []
            cross_mae = []
            # 5 fold cross validate
            for k in range(5):
                X_train, X_test, y_train, y_test = train_test_split(
                    smt.add_constant(data[np.append(best_labels, label)]), data_labels,
                    test_size=0.20, random_state=0)
                clf = OLS(y_train, X_train).fit()
                y_pred = clf.predict(X_test)
                cross_r_squared.append(clf.rsquared)
                cross_aics.append(clf.aic)
                cross_bics.append(clf.bic)
                cross_mae.append(mean_absolute_error(y_test, y_pred))
            r_squared.append(np.mean(cross_r_squared))
            aics.append(np.mean(cross_aics))
            bics.append(np.mean(cross_bics))
            maes.append(np.mean(cross_mae))
        # Find the min loss fit
        min_ind = np.argmax(r_squared)
        # Update the output values
        best_r_squared.append(r_squared[min_ind])
        best_aics.append(aics[min_ind])
        best_bics.append(bics[min_ind])
        best_maes.append(maes[min_ind])
        # Update best labels and labels
        best_labels = np.append(best_labels, labels[min_ind])
        labels = np.delete(labels, [min_ind])
    return best_labels, best_r_squared, best_aics, best_bics, best_maes

data_columns = methyl.columns[1:][::-1][1:][::-1]
methyl = pd.read_csv("small_met.csv", sep='\t')
methyl_values = methyl.values[:, 1:methyl.columns.size-1]
ages = methyl['age'].values

labels, r_squared, aics, bics, maes = scikit_iteratively_select_variables_with_cross_validation(
    methyl[data_columns], ages, max_variables=150)

Variables:  1	Variables:  2	Variables:  3	Variables:  4	Variables:  5	Variables:  6	Variables:  7	Variables:  8	Variables:  9	Variables:  10	Variables:  11	Variables:  12	Variables:  13	Variables:  14	Variables:  15	Variables:  16	Variables:  17	Variables:  18	Variables:  19	Variables:  20	Variables:  21	Variables:  22	Variables:  23	Variables:  24	Variables:  25	Variables:  26	Variables:  27	Variables:  28	Variables:  29	Variables:  30	Variables:  31	Variables:  32	Variables:  33	Variables:  34	Variables:  35	Variables:  36	Variables:  37	Variables:  38	Variables:  39	Variables:  40	Variables:  41	Variables:  42	Variables:  43	Variables:  44	Variables:  45	Variables:  46	Variables:  47	Variables:  48	Variables:  49	Variables:  50	Variables:  51	Variables:  52	Variables:  53	Variables:  54	Variables:  55	Variables:  56	Variables:  57	Variables:  58	Variables:  59	Variables:  60	Variables:  61	Variables:  62	Variables:  63	Variables:  64	Variables:  65	Variables:  66	Variables:  67	Variables:  68	Variables:  69	Variables:  70	Variables:  71	Variables:  72	Variables:  73	Variables:  74	Variables:  75	Variables:  76	Variables:  77	Variables:  78	Variables:  79	Variables:  80	Variables:  81	Variables:  82	Variables:  83	Variables:  84	Variables:  85	Variables:  86	Variables:  87	Variables:  88	Variables:  89	Variables:  90	Variables:  91	Variables:  92	Variables:  93	Variables:  94	Variables:  95	Variables:  96	Variables:  97	Variables:  98	Variables:  99	Variables:  100	Variables:  101	Variables:  102	Variables:  103	Variables:  104	Variables:  105	Variables:  106	Variables:  107	Variables:  108	Variables:  109	Variables:  110	Variables:  111	Variables:  112	Variables:  113	Variables:  114	Variables:  115	Variables:  116	Variables:  117	Variables:  118	Variables:  119	Variables:  120	Variables:  121	Variables:  122	Variables:  123	Variables:  124	Variables:  125	Variables:  126	Variables:  127	Variables:  128	Variables:  129	Variables:  130	Variables:  131	Variables:  132	Variables:  133	Variables:  134	Variables:  135	Variables:  136	Variables:  137	Variables:  138	Variables:  139	Variables:  140	Variables:  141	Variables:  142	Variables:  143	Variables:  144	Variables:  145	Variables:  146	Variables:  147	Variables:  148	Variables:  149	Variables:  150	

def plot_r2_aics_bics_maes_data(r2, aics, bics, maes, max_variables):
    plt.figure(figsize=(15, 15))
    x = range(max_variables)
    xx = range(0,max_variables,max_variables//10)
    # Loss function
    plt.subplot("221")
    plt.plot(x, r2, 'ro--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('r2')
    plt.xticks(xx)
    plt.title("r-squared function")
    # AIC function
    plt.subplot("222")
    plt.plot(x, aics, 'ro--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('AIC')
    plt.xticks(xx)
    plt.title("AIC function")
    # BIC function
    plt.subplot("223")
    plt.plot(x, bics, 'go--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('BIC')
    plt.xticks(xx)
    plt.title("BIC function")
    # AUC function
    plt.subplot("224")
    plt.plot(x, maes, 'bo--', linewidth=1, markersize=7)
    plt.xlabel('# of variables')
    plt.ylabel('MAE')
    plt.xticks(xx)
    plt.title("MAE function")

plot_r2_aics_bics_maes_data(r_squared, aics, bics, maes, 150)

png

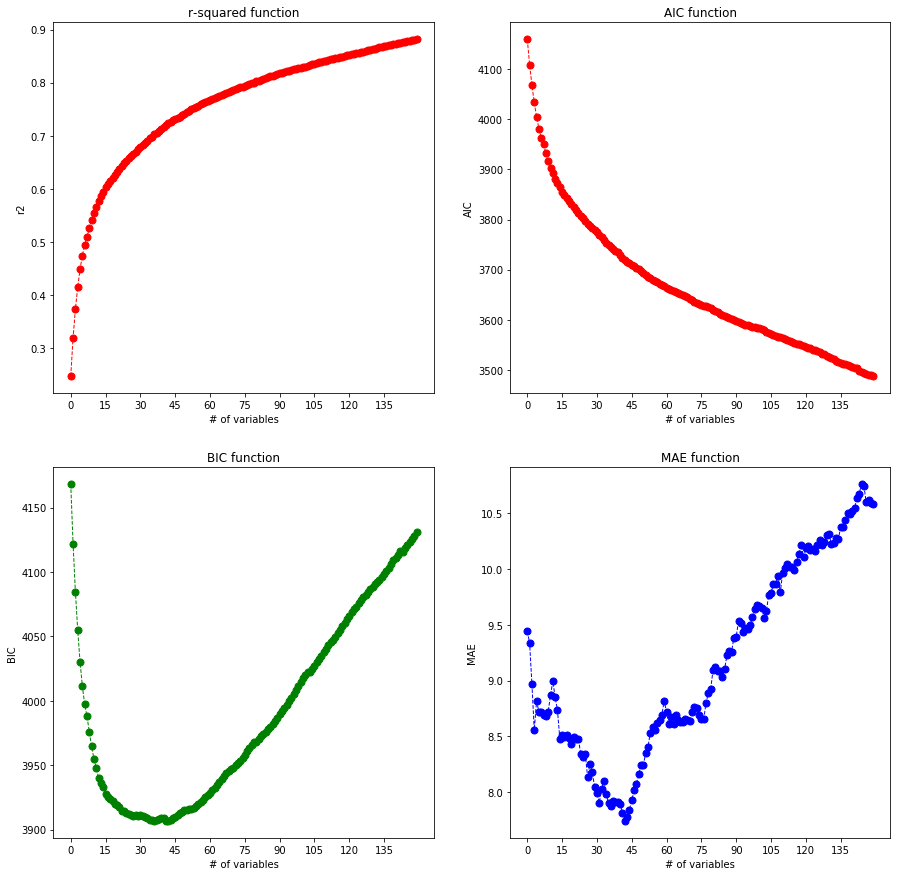
It can be seen that BIC and MAE have their minima at around 42 but AIC is constantly getting smaller, meanwhile r-squared is approaching 1 thus the fit is getting better. Selecting the minimum of the returned BIC and MAE arrays I’m going to take the average of their minimum index and select that as best iterative parameter.

min_bic_ind = np.argmin(bics)
min_mae_ind = np.argmin(maes)
min_ind = max(min_bic_ind, min_mae_ind, (min_bic_ind+min_mae_ind)//2)
min_ind

Obviously this MUST be right since it happened to be 42, I should have expected that to be the case all along. Doing the OLS fit with these parameters:

best_labels = labels[:min_ind]
methyl = pd.read_csv("small_met.csv", sep='\t')
methyl_values = methyl[best_labels].values
ages = methyl['age'].values

X_train, X_test, y_train, y_test = train_test_split(
                    smt.add_constant(methyl_values), ages,
                    test_size=0.20, random_state=0)

model = OLS(y_train, X_train).fit()
pred_train = model.predict(X_train)
pred_test = model.predict(X_test)

plot_predictions(y_train, pred_train)

png

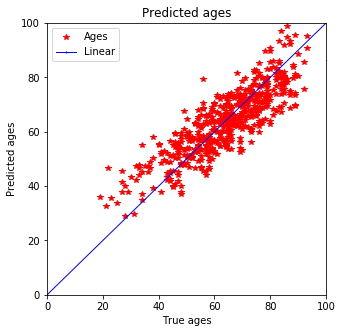
plot_predictions(y_test, pred_test)

png

Expecting it qualitatively this prediction seems better than the one with Ridge estimation. Not only does the training data fit better but also the testing data shows smaller discrepancy for younger peoply. Previously a tail was predicted for people below 40 but now that is defeinetly smaller and most of the data is in 3$\sigma$.

@Regards, Alex

Alex Olar

Christian, foodie, physicist, tech enthusiast

Getting acquainted with different regression models using scientific data from different sources

Subset selection, regularization

@Regards, Alex

Related Posts

Alex Olar