Linear methods in classification
- 31 minsLinear methods in classification
1, Load data
- (A), Download data from http://science.sciencemag.org/content/early/2018/01/17/science.aar3247
- (B), Load protein levels, and convert them to numerical values if necessary
- (C), Inspect missing values, and drop patients with missing values in protein levels
- (D), Load cancer labels
2, Logisic regression with Statsmodels
- (A), Fit a logistic regression using statsmodels to cancer/normal binary labels using protein levels as inputs
- (B), Evaluate the logloss and the accuracy of the fit.
- (C), Evaluate the ROC, and AUC of the fit.
3, Hepatocellular carcinoma
- (A), Fit a logistic regression using statsmodels to Hepatocellular carcinoma (liver cancer)/normal binary labels.
- (B), Select the 4 most significant proteins and repeat the fit.
- (C), Select the 1 most significant protein and repeat the fit.
- (D), Compare the ROC, and AUC of the fits with 4 and 1 proteins. Which would you use when screening for cancers?
- (E), Interpret the results using the wikipedia page of Hepatocellular carcinoma.
4, Cross validation
- (A), Fit logistic regression using statsmodels to cancer/normal binary labels using protein levels as inputs using 5 fold cross-validation
- (B), Calculate the mean and the std of AUC values for the 5 folds, and plot the 5 ROC curves on the same plot.
5, Sklearn
- (A), Fit a logistic regression using scikit-learn to cancer/normal binary labels using protein levels as inputs
- (B), Compare the coefficient with the statsmodels output, are they the same? If not why not?
- (C), Fit logistic regression using sklearn to cancer/normal binary labels using protein levels as inputs using 5 fold cross-validation, Calculate the mean and the std of AUC values for the 5 folds, and plot the 5 ROC curves on the same plot.
- (D), Fit linear discriminant analysis using sklearn to cancer/normal binary labels using protein levels as inputs using 5 fold cross-validation, Calculate the mean and the std of AUC values for the 5 folds, and plot the 5 ROC curves on the same plot. Is it better than logistic regression?
- (E), Fit a logistic regression using scikit-learn to the multi class problem with a different class for each cancer type and one for normals. Evaluate predictions with the confusion matrix, interpret the result matrix.
1. Loading data
%pylab inline
import pandas as pd
from sklearn import metrics as ms
Populating the interactive namespace from numpy and matplotlib
xls = pd.ExcelFile('aar3247_Cohen_SM_Tables-S1-S11.xlsx') # modified excel file
proteins = pd.read_excel(xls, 'Table S3')
protein_levels = pd.read_excel(xls, 'Table S6')
cancerTypes = pd.read_excel(xls, 'Table S11')
protein_levels.columns.values
array(['Patient ID #', 'Sample ID #', 'Tumor type', 'AJCC Stage',
'AFP (pg/ml)', 'Angiopoietin-2 (pg/ml)', 'AXL (pg/ml)',
'CA-125 (U/ml)', 'CA 15-3 (U/ml)', 'CA19-9 (U/ml)', 'CD44 (ng/ml)',
'CEA (pg/ml)', 'CYFRA 21-1 (pg/ml)', 'DKK1 (ng/ml)',
'Endoglin (pg/ml)', 'FGF2 (pg/ml)', 'Follistatin (pg/ml)',
'Galectin-3 (ng/ml)', 'G-CSF (pg/ml)', 'GDF15 (ng/ml)',
'HE4 (pg/ml)', 'HGF (pg/ml)', 'IL-6 (pg/ml)', 'IL-8 (pg/ml)',
'Kallikrein-6 (pg/ml)', 'Leptin (pg/ml)', 'Mesothelin (ng/ml)',
'Midkine (pg/ml)', 'Myeloperoxidase (ng/ml)', 'NSE (ng/ml)',
'OPG (ng/ml)', 'OPN (pg/ml)', 'PAR (pg/ml)', 'Prolactin (pg/ml)',
'sEGFR (pg/ml)', 'sFas (pg/ml)', 'SHBG (nM)',
'sHER2/sEGFR2/sErbB2 (pg/ml)', 'sPECAM-1 (pg/ml)', 'TGFa (pg/ml)',
'Thrombospondin-2 (pg/ml)', 'TIMP-1 (pg/ml)', 'TIMP-2 (pg/ml)',
'CancerSEEK Logistic Regression Score', 'CancerSEEK Test Result'],
dtype=object)
tumorsAndProteinLevels = np.array(['Tumor type','AFP (pg/ml)', 'Angiopoietin-2 (pg/ml)', 'AXL (pg/ml)',
'CA-125 (U/ml)', 'CA 15-3 (U/ml)', 'CA19-9 (U/ml)', 'CD44 (ng/ml)','CEA (pg/ml)', 'CYFRA 21-1 (pg/ml)',
'DKK1 (ng/ml)', 'Endoglin (pg/ml)', 'FGF2 (pg/ml)', 'Follistatin (pg/ml)', 'Galectin-3 (ng/ml)',
'G-CSF (pg/ml)', 'GDF15 (ng/ml)', 'HE4 (pg/ml)', 'HGF (pg/ml)', 'IL-6 (pg/ml)', 'IL-8 (pg/ml)',
'Kallikrein-6 (pg/ml)', 'Leptin (pg/ml)', 'Mesothelin (ng/ml)', 'Midkine (pg/ml)', 'Myeloperoxidase (ng/ml)',
'NSE (ng/ml)', 'OPG (ng/ml)', 'OPN (pg/ml)', 'PAR (pg/ml)', 'Prolactin (pg/ml)', 'sEGFR (pg/ml)',
'sFas (pg/ml)', 'SHBG (nM)', 'sHER2/sEGFR2/sErbB2 (pg/ml)', 'sPECAM-1 (pg/ml)', 'TGFa (pg/ml)',
'Thrombospondin-2 (pg/ml)', 'TIMP-1 (pg/ml)', 'TIMP-2 (pg/ml)'])
# Remove * and ** values
plvls = protein_levels[tumorsAndProteinLevels].applymap(lambda x: float(x[2:]) if type(x)==str and x[0:2]=="**" else x)
plvls = plvls.applymap(lambda x: float(x[1:]) if type(x)==str and x[0:1]=="*" else x)
# Drop rows containing NaN or missing value
plvls = plvls.dropna(axis='rows')
# Extract cancer types for all the corresponding protein levels
cancer_types = np.array(list(map(lambda x: 1 if x=="Normal" else 0, plvls['Tumor type'].values)))
plvls = plvls[tumorsAndProteinLevels[1:]].values
# normalizing the data (subtracting the mean, division by standard deviation and rescaling)
from sklearn.preprocessing import normalize
plvls = normalize(plvls, axis=1)
2. Logistic regression with the Statsmodels package
import statsmodels.formula.api as sm
import statsmodels.tools as smt
from sklearn.model_selection import train_test_split
# Splitting the randomized data 20%-80%
X_train, X_test, y_train, y_test = train_test_split(
smt.add_constant(plvls), cancer_types, test_size=0.20, random_state=42)
# Logistic model on binary cancer -> healthy or not
logistic_model = sm.Logit(y_train, X_train)
# basinhopping seems to be the best option
results = logistic_model.fit(method='basinhopping', full_output=True, disp=False)
# result summmary with quite a lot of significant values
print(results.summary())
Logit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 1442
Model: Logit Df Residuals: 1402
Method: MLE Df Model: 39
Date: Mon, 15 Oct 2018 Pseudo R-squ.: 0.5260
Time: 21:42:46 Log-Likelihood: -469.52
converged: True LL-Null: -990.62
LLR p-value: 3.346e-193
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
const 0.6000 1.131 0.530 0.596 -1.618 2.818
x1 -3.5770 2.088 -1.713 0.087 -7.670 0.516
x2 -5.3194 7.453 -0.714 0.475 -19.928 9.289
x3 8.2998 8.143 1.019 0.308 -7.660 24.259
x4 -1073.4014 871.421 -1.232 0.218 -2781.355 634.552
x5 135.4893 536.920 0.252 0.801 -916.855 1187.833
x6 -2660.3710 716.920 -3.711 0.000 -4065.508 -1255.234
x7 717.5979 1090.987 0.658 0.511 -1420.697 2855.892
x8 -16.3977 5.892 -2.783 0.005 -27.947 -4.849
x9 -17.9177 7.834 -2.287 0.022 -33.271 -2.564
x10 60.2152 2.7e+04 0.002 0.998 -5.28e+04 5.29e+04
x11 34.0421 11.405 2.985 0.003 11.688 56.396
x12 678.2362 153.364 4.422 0.000 377.648 978.824
x13 -27.2716 14.017 -1.946 0.052 -54.745 0.201
x14 163.1523 2113.828 0.077 0.938 -3979.874 4306.179
x15 -14.8799 36.669 -0.406 0.685 -86.750 56.990
x16 -29.5278 2.1e+04 -0.001 0.999 -4.12e+04 4.11e+04
x17 -4.1072 3.054 -1.345 0.179 -10.094 1.879
x18 -86.3493 107.532 -0.803 0.422 -297.107 124.409
x19 -2646.5090 490.893 -5.391 0.000 -3608.641 -1684.376
x20 109.3728 268.396 0.408 0.684 -416.675 635.420
x21 13.7720 3.926 3.508 0.000 6.076 21.468
x22 -0.0812 0.650 -0.125 0.901 -1.354 1.192
x23 -146.5316 675.869 -0.217 0.828 -1471.211 1178.148
x24 -16.7786 11.043 -1.519 0.129 -38.423 4.866
x25 -1014.3083 332.890 -3.047 0.002 -1666.761 -361.855
x26 1859.2179 587.054 3.167 0.002 708.613 3009.823
x27 -71.5914 1.09e+04 -0.007 0.995 -2.15e+04 2.14e+04
x28 -3.6120 0.752 -4.804 0.000 -5.086 -2.138
x29 1.2209 2.400 0.509 0.611 -3.483 5.924
x30 -4.7926 0.713 -6.723 0.000 -6.190 -3.395
x31 47.3033 8.832 5.356 0.000 29.993 64.614
x32 6.0481 3.123 1.936 0.053 -0.074 12.170
x33 -242.2809 129.592 -1.870 0.062 -496.277 11.715
x34 -7.7019 5.879 -1.310 0.190 -19.225 3.821
x35 15.2673 5.866 2.602 0.009 3.769 26.765
x36 532.4986 362.637 1.468 0.142 -178.256 1243.253
x37 0.1656 1.496 0.111 0.912 -2.767 3.098
x38 -2.8102 0.912 -3.083 0.002 -4.597 -1.023
x39 4.1496 1.068 3.887 0.000 2.057 6.242
==============================================================================
# logloss is the negative loglike function
logloss = -logistic_model.loglike(results.params)
print("Logloss :", logloss)
Logloss : 469.52213049392526
train_prediction = results.predict(X_test)
pred = train_prediction
truth = y_test
print("Accuracy %.1f%%" %
(100.*ms.accuracy_score(truth, np.array(list(map(lambda x: 1 if x > 0.5 else 0, train_prediction))))))
Accuracy 84.2%
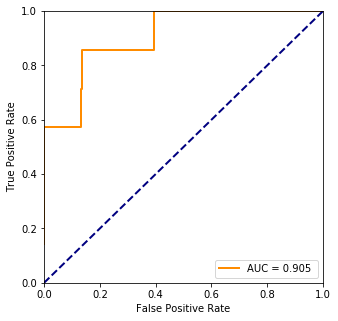
fpr, tpr, threshold = ms.roc_curve(truth, pred)
plt.figure(figsize=(5.,5.))
lw = 2
plt.plot(fpr, tpr, color='darkorange',lw=lw, label="AUC = %.3f " % ms.auc(fpr, tpr))
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc="lower right")
plt.show()
3. Hepatocellular carcinoma
# Remove * and ** values
plvls = protein_levels[tumorsAndProteinLevels].applymap(lambda x: float(x[2:]) if type(x)==str and x[0:2]=="**" else x)
plvls = plvls.applymap(lambda x: float(x[1:]) if type(x)==str and x[0:1]=="*" else x)
# Drop rows containing NaN or missing value
plvls = plvls.dropna(axis='rows')
# Extract lung cancer and healthy statistics for all the corresponding protein levels
# lung_cancers = plvls.loc[plvls['Tumor type'] == 'Lung']
# no_cancers = plvls.loc[plvls['Tumor type'] == 'Normal']
# concat dataframes
df = plvls
cancers = np.array(list(map(lambda x: 1 if x=="Liver" else 0, df['Tumor type'].values)))
plevels = normalize(df.values[:,1:])
# Splitting the randomized data 20%-80%
X_train, X_test, y_train, y_test = train_test_split(
plevels, cancers, test_size=0.20, random_state=42)
# Logistic model on binary cancer -> healthy or not
logistic_model = sm.Logit(y_train, X_train)
# basinhopping seems to be the best option
results = logistic_model.fit(method='basinhopping', full_output=True, disp=False)
# result summmary with quite a lot of significant values
print(results.summary())
Logit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 1442
Model: Logit Df Residuals: 1403
Method: MLE Df Model: 38
Date: Mon, 15 Oct 2018 Pseudo R-squ.: 0.4477
Time: 21:42:54 Log-Likelihood: -95.026
converged: True LL-Null: -172.05
LLR p-value: 6.551e-16
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
x1 3.7276 1.057 3.527 0.000 1.656 5.799
x2 -8.6690 19.760 -0.439 0.661 -47.398 30.060
x3 6.5320 29.560 0.221 0.825 -51.404 64.468
x4 6.0267 451.962 0.013 0.989 -879.802 891.856
x5 -0.6295 645.145 -0.001 0.999 -1265.090 1263.831
x6 6.6919 79.444 0.084 0.933 -149.016 162.400
x7 1.6491 4562.877 0.000 1.000 -8941.425 8944.723
x8 -1.4322 2.083 -0.687 0.492 -5.516 2.651
x9 -4.5182 5.120 -0.883 0.378 -14.553 5.516
x10 1.3307 1.17e+05 1.13e-05 1.000 -2.3e+05 2.3e+05
x11 52.0444 18.659 2.789 0.005 15.473 88.615
x12 -1.3780 668.740 -0.002 0.998 -1312.084 1309.328
x13 -66.7710 69.069 -0.967 0.334 -202.144 68.602
x14 1.6982 4602.218 0.000 1.000 -9018.483 9021.879
x15 -36.5254 119.068 -0.307 0.759 -269.895 196.844
x16 4.7640 4.67e+04 0.000 1.000 -9.16e+04 9.16e+04
x17 -45.2825 29.314 -1.545 0.122 -102.737 12.172
x18 26.4487 133.842 0.198 0.843 -235.877 288.775
x19 7.3615 587.364 0.013 0.990 -1143.850 1158.573
x20 -15.1498 219.199 -0.069 0.945 -444.772 414.472
x21 8.7405 14.674 0.596 0.551 -20.020 37.501
x22 -3.0883 1.520 -2.032 0.042 -6.067 -0.109
x23 -3.2841 3232.644 -0.001 0.999 -6339.150 6332.582
x24 -51.6663 74.528 -0.693 0.488 -197.739 94.406
x25 5.4704 488.129 0.011 0.991 -951.245 962.186
x26 -7.3590 2207.177 -0.003 0.997 -4333.347 4318.629
x27 4.1483 4.9e+04 8.46e-05 1.000 -9.61e+04 9.61e+04
x28 1.2979 0.858 1.513 0.130 -0.384 2.979
x29 -14.2841 12.416 -1.150 0.250 -38.620 10.051
x30 -0.2821 0.648 -0.435 0.663 -1.552 0.988
x31 -91.1302 49.350 -1.847 0.065 -187.854 5.593
x32 0.0814 14.340 0.006 0.995 -28.025 28.188
x33 -4.9679 782.216 -0.006 0.995 -1538.083 1528.148
x34 7.0201 19.479 0.360 0.719 -31.158 45.199
x35 -22.0093 26.141 -0.842 0.400 -73.245 29.226
x36 1.5358 2830.114 0.001 1.000 -5545.385 5548.456
x37 6.9943 2.144 3.262 0.001 2.792 11.197
x38 -1.6280 1.123 -1.450 0.147 -3.829 0.573
x39 -0.3257 3.186 -0.102 0.919 -6.571 5.919
==============================================================================
Possibly complete quasi-separation: A fraction 0.19 of observations can be
perfectly predicted. This might indicate that there is complete
quasi-separation. In this case some parameters will not be identified.
# logloss is the negative loglike function
logloss = -logistic_model.loglike(results.params)
print("Logloss :", logloss)
train_prediction = results.predict(X_test)
pred = train_prediction
truth = y_test
print("Accuracy %.1f%%" %
(100.*ms.accuracy_score(truth, np.array(list(map(lambda x: 1 if x > 0.5 else 0, train_prediction))))))
Logloss : 95.02632456837271
Accuracy 99.2%
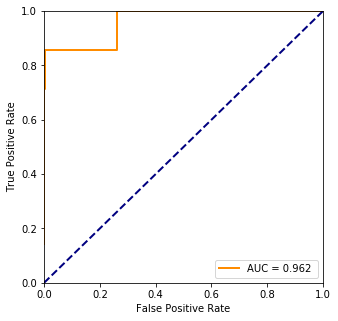
fpr, tpr, threshold = ms.roc_curve(truth, pred)
plt.figure(figsize=(5.,5.))
lw = 2
plt.plot(fpr, tpr, color='darkorange',lw=lw, label="AUC = %.3f " % ms.auc(fpr, tpr))
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc="lower right")
plt.show()
# Most significant protein levels
ind = results.pvalues.argsort()[:4]
print(ind)
sign_plevels = plevels[:, ind]
sign_plevels
[ 0 36 10 21]
array([[0.01308731, 0.18070516, 0.02382528, 0.62671162],
[0.00297345, 0.12333307, 0.01630231, 0.88022385],
[0.04177204, 0.05760751, 0.02306187, 0.02567324],
...,
[0.00306925, 0.00209177, 0.00174422, 0.03738842],
[0.00365565, 0.02853169, 0.0092258 , 0.02688729],
[0.00422653, 0.06188239, 0.00841454, 0.44904901]])
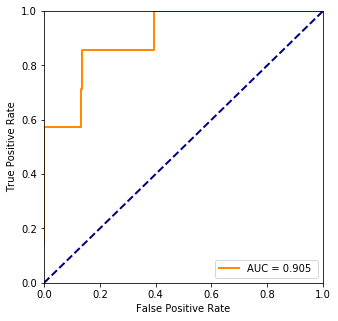
The most significant value seems to be at index 0 which is the first row from plvls thus it is the AFP protein’s level. It is confirmed by the wikipedia page as well that it is an indicator of lung cancer. However, even though the accuracy of the predicted values is good, the model is not and that can be seen on the ROC curve.
# Redoing the fit and everything
# Splitting the randomized data 20%-80%
X_train, X_test, y_train, y_test = train_test_split(
sign_plevels, cancers, test_size=0.20, random_state=42)
# Logistic model on binary cancer -> healthy or not
logistic_model = sm.Logit(y_train, X_train)
# basinhopping seems to be the best option
results = logistic_model.fit(method='basinhopping', full_output=True, disp=False)
# result summmary with quite a lot of significant values
print(results.summary())
# logloss is the negative loglike function
logloss = -logistic_model.loglike(results.params)
print("Logloss :", logloss)
train_prediction = results.predict(X_test)
pred = train_prediction
truth = y_test
print("Accuracy %.1f%%" %
(100.*ms.accuracy_score(truth, np.array(list(map(lambda x: 1 if x > 0.5 else 0, train_prediction))))))
fpr, tpr, threshold = ms.roc_curve(truth, pred)
plt.figure(figsize=(5.,5.))
lw = 2
plt.plot(fpr, tpr, color='darkorange',lw=lw, label="AUC = %.3f " % ms.auc(fpr, tpr))
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc="lower right")
plt.show()
Logit Regression Results
==============================================================================
Dep. Variable: y No. Observations: 1442
Model: Logit Df Residuals: 1438
Method: MLE Df Model: 3
Date: Mon, 15 Oct 2018 Pseudo R-squ.: 0.03755
Time: 21:42:55 Log-Likelihood: -165.59
converged: True LL-Null: -172.05
LLR p-value: 0.004814
==============================================================================
coef std err z P>|z| [0.025 0.975]
------------------------------------------------------------------------------
x1 3.7369 0.911 4.102 0.000 1.951 5.522
x2 0.3410 2.426 0.141 0.888 -4.415 5.097
x3 -240.7636 25.488 -9.446 0.000 -290.720 -190.808
x4 -9.2729 2.208 -4.201 0.000 -13.600 -4.946
==============================================================================
Possibly complete quasi-separation: A fraction 0.18 of observations can be
perfectly predicted. This might indicate that there is complete
quasi-separation. In this case some parameters will not be identified.
Logloss : 165.58768191156673
Accuracy 98.6%
4. Cross validation
# Remove * and ** values
plvls = protein_levels[tumorsAndProteinLevels].applymap(lambda x: float(x[2:]) if type(x)==str and x[0:2]=="**" else x)
plvls = plvls.applymap(lambda x: float(x[1:]) if type(x)==str and x[0:1]=="*" else x)
# Drop rows containing NaN or missing value
plvls = plvls.dropna(axis='rows')
# Extract cancer types for all the corresponding protein levels
cancer_types = np.array(list(map(lambda x: 1 if x=="Normal" else 0, plvls['Tumor type'].values)))
plvls = plvls[tumorsAndProteinLevels[1:]].values
# Normalizing the values as well
plvls = normalize(plvls, axis=1)
# Cross validate
def cross_validate(plvls, cancer_types, k_fold=5):
logloss = []
accuracy = []
fpr = dict()
tpr = dict()
auc = []
for i in range(k_fold):
# Splitting the randomized data 20%-80%
X_train, X_test, y_train, y_test = train_test_split(plvls, cancer_types,
test_size=1./k_fold,
random_state=42*i + (137-i)*k_fold)
# Logistic model on binary cancer -> healthy or not
logistic_model = sm.Logit(y_train, X_train)
# basinhopping seems to be the best option
results = logistic_model.fit(method='basinhopping', full_output=True, disp=False)
# logloss is the negative loglike function
logloss.append(-logistic_model.loglike(results.params))
train_prediction = results.predict(X_test)
pred = train_prediction
truth = y_test
accuracy.append(100.*ms.accuracy_score(truth, np.array(list(map(lambda x: 1 if x > 0.5 else 0, train_prediction)))))
fpr[i], tpr[i], threshold = ms.roc_curve(truth, pred)
auc.append(ms.auc(fpr[i], tpr[i]))
return logloss, accuracy, auc, fpr, tpr
def plot_cross_validated_data(values, k_fold=5):
logloss, accuracy, auc, fpr, tpr = values
print("Mean Accuracy = %.1f%%" % np.mean(accuracy))
if(len(logloss) > 0):
print("\t\t Mean logloss = %.3f" % np.mean(logloss))
plt.figure(figsize=(8.,8.))
lw = 2
cmap = ['r', 'g', 'b', 'c', 'darkorange']
for i in range(k_fold):
plt.plot(fpr[i], tpr[i], color=cmap[i%5],lw=lw, linestyle='--', label="AUC = %.3f " % auc[i])
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='-', label="Mean AUC = %.3f +/- %.3f" %
(np.mean(auc), np.std(auc)))
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.0])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.legend(loc="lower right")
plt.show()
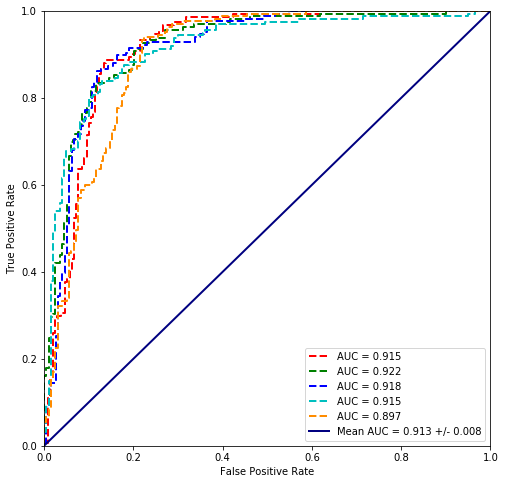
values = cross_validate(plvls, cancer_types)
plot_cross_validated_data(values)
Mean Accuracy = 85.1%
Mean logloss = 470.434
5. Scikit comparison
from sklearn.linear_model import LogisticRegression
# Splitting the randomized data 20%-80%
X_train, X_test, y_train, y_test = train_test_split(plvls, cancer_types,
test_size=0.2, random_state=42)
clf = LogisticRegression(random_state=137, solver='lbfgs').fit(X_train, y_train)
clf.coef_
array([[-9.48707744e-01, 1.83903929e-02, 7.95491459e-01,
-2.52954480e-02, 3.05955892e-04, -7.56440297e-02,
9.15254779e-03, -2.67799468e+00, -8.16559492e-01,
6.23163704e-04, 9.88404739e-01, 4.74152986e-02,
1.17032345e-01, 7.70760276e-04, -9.34918494e-03,
-3.84480629e-04, -7.18391518e-01, -9.01026951e-02,
-3.18421447e-02, -7.51784431e-03, 2.11467676e+00,
1.16728461e+00, 1.90117408e-03, -3.44293734e-01,
-2.54546830e-02, 1.85846906e-02, -2.52367752e-04,
-2.46246869e+00, 1.74366466e+00, -2.97473230e+00,
2.01660531e+00, 1.33148112e+00, 9.52140907e-04,
1.83475532e+00, 2.70761855e+00, 1.27181348e-02,
2.10712966e-01, -7.35910282e-01, 5.88527779e+00]])
smclf = sm.Logit(y_train, X_train).fit(method='basinhopping', full_output=True, disp=False)
smclf.params
array([-3.22387768e+00, -4.82459242e+00, 8.47257625e+00, -1.07291690e+03,
1.43809357e+02, -2.64476560e+03, 7.15330113e+02, -1.65885994e+01,
-1.79806999e+01, 5.33958704e+01, 3.35214507e+01, 6.72095874e+02,
-2.67618774e+01, 1.62104363e+02, -1.28811089e+01, -2.54467653e+01,
-3.85213260e+00, -9.54969343e+01, -2.63774649e+03, 1.19648533e+02,
1.37009167e+01, 2.31513267e-01, -1.39479210e+02, -1.73462433e+01,
-1.01227642e+03, 1.86133386e+03, -6.88544270e+01, -3.27699019e+00,
1.23930995e+00, -4.50896105e+00, 4.67843272e+01, 6.10458336e+00,
-2.48495710e+02, -7.98193338e+00, 1.55007443e+01, 5.25445783e+02,
3.22225689e-01, -2.42487203e+00, 4.41508794e+00])
They differ so maybe the problem doesn’t have one solution or doesn’t have one best solution. Also the methods with which they are looking for a solution differ as well. (Update: it turned out that they differ because scikit learn is using regulization by default. )
# Cross validate
def scikit_cross_validate(model, plvls, cancer_types, k_fold=5):
logloss = []
accuracy = []
fpr = dict()
tpr = dict()
auc = []
for i in range(k_fold):
# Splitting the randomized data 20%-80%
X_train, X_test, y_train, y_test = train_test_split(plvls, cancer_types,
test_size=1./k_fold,
random_state=137*i + i*42, shuffle=True)
# Logistic model on binary cancer -> healthy or not
clf = model.fit(X_train, y_train)
train_prediction = clf.predict(X_test)
pred_value = clf.decision_function(X_test)
pred = train_prediction
truth = y_test
accuracy.append(100.*ms.accuracy_score(truth, train_prediction))
fpr[i], tpr[i], threshold = ms.roc_curve(truth, pred_value)
auc.append(ms.auc(fpr[i], tpr[i]))
return logloss, accuracy, auc, fpr, tpr
values = scikit_cross_validate(LogisticRegression(random_state=42, solver='newton-cg'), plvls, cancer_types)
plot_cross_validated_data(values)
Mean Accuracy = 79.3%
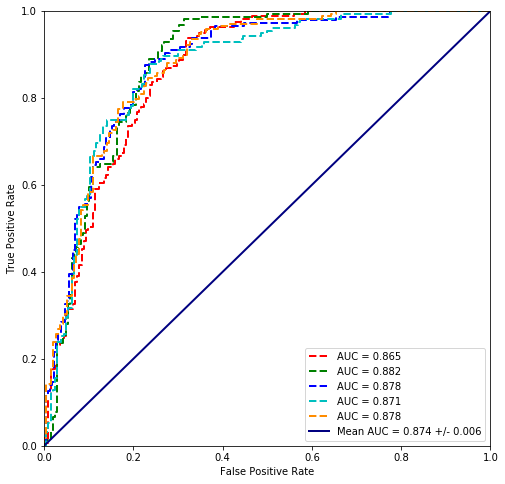
The results with scikit are ‘worse’ however the minimization method is different so Statsmodels and Scikit must get different solutions.
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
values = scikit_cross_validate(LinearDiscriminantAnalysis(), plvls, cancer_types)
plot_cross_validated_data(values)
Mean Accuracy = 84.0%
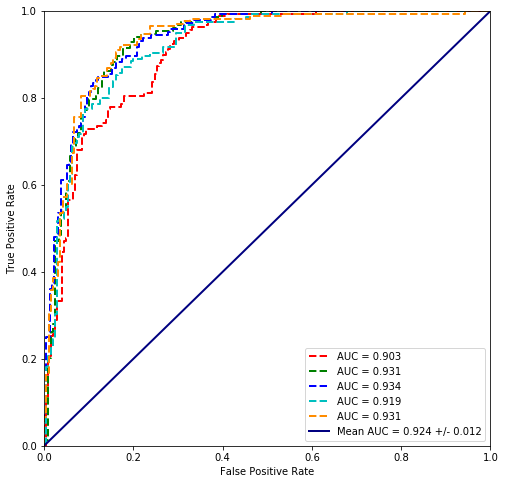
Linear discriminant analysis seems to fit the data best so far.
# Remove * and ** values
plvls = protein_levels[tumorsAndProteinLevels].applymap(lambda x: float(x[2:]) if type(x)==str and x[0:2]=="**" else x)
plvls = plvls.applymap(lambda x: float(x[1:]) if type(x)==str and x[0:1]=="*" else x)
# Drop rows containing NaN or missing value
plvls = plvls.dropna(axis='rows')
# Extract cancer types for all the corresponding protein levels
cancer_types = plvls['Tumor type'].values
plvls = plvls[tumorsAndProteinLevels[1:]].values
# Splitting the randomized data 20%-80%
X_train, X_test, y_train, y_test = train_test_split(plvls, cancer_types,
test_size=0.2, random_state=42)
clf = LogisticRegression(random_state=137, solver='lbfgs', multi_class='multinomial').fit(X_train, y_train)
pred = clf.predict(X_test)
conf_matrix = ms.confusion_matrix(y_test, pred, labels=clf.classes_)
conf_matrix
array([[ 12, 11, 0, 0, 0, 22, 1, 3, 0],
[ 3, 43, 0, 0, 4, 16, 1, 0, 2],
[ 0, 10, 1, 0, 0, 3, 0, 1, 0],
[ 0, 1, 0, 4, 0, 0, 0, 1, 1],
[ 1, 10, 0, 0, 4, 4, 0, 1, 0],
[ 3, 5, 0, 0, 1, 148, 0, 0, 1],
[ 0, 4, 0, 0, 1, 1, 3, 0, 1],
[ 0, 3, 0, 0, 0, 15, 1, 2, 0],
[ 2, 7, 0, 0, 0, 1, 0, 0, 2]])
import itertools
conf_matrix = normalize(conf_matrix)
plt.figure(figsize=(10.,10.))
plt.imshow(conf_matrix, interpolation='nearest', cmap=plt.cm.Blues)
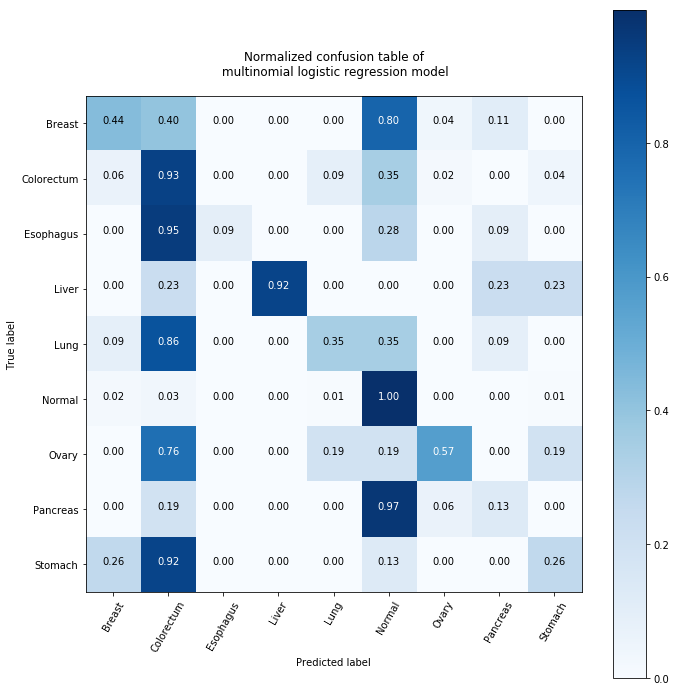
plt.title("Normalized confusion table of\n multinomial logistic regression model\n")
plt.colorbar()
tick_marks = np.arange(clf.classes_.size)
plt.xticks(tick_marks, clf.classes_, rotation=60)
plt.yticks(tick_marks, clf.classes_)
fmt = '.2f'
thresh = conf_matrix.max() / 2.
for i, j in itertools.product(range(conf_matrix.shape[0]), range(conf_matrix.shape[1])):
plt.text(j, i, format(conf_matrix[i, j], fmt), horizontalalignment="center",
color="white" if conf_matrix[i, j] > thresh else "black")
plt.ylabel('True label')
plt.xlabel('Predicted label')
plt.tight_layout()
What we can learn from this? It is clear that our prediction is not that good. We predicted most of the healthy people helathy but we predicted most of the patients with Pancreas cancer healthy. Not only could we not figure out too well the cancers but also the model categorized most of cancers as Colorectum, however, I must mention that most of cancers is indeed colorectum so our model is not a complete failure.
It is also intersting that the model was capeable of identifying breast and ovary cancer pretty well and even liver cancer was identified quiet well.
@Regards, Alex
Alex Olar
Christian, foodie, physicist, tech enthusiast