Fast neural style transfer

Friday. November 22, 2019 - 5 mins

Neural style transfer

I wrote about neural style transfer previously in this blog post and recently I found an article which is by no means recent but fascinated me. Machine learning can be great fun and people are doing loads of stuff in this filed that is suprisingly original. When I tumbled upon J.C. Johnson’s et al. article) about fast neural style transfer I was eager to understand it.

The main point of neural style transfer was that the algorithm optimized one image with many iterations in order to transfer the style of an other image to it. This is a quite long iterative process but the results are worth it.

It would be nice to do it in a feed-forward way, wouldn’t it? Maybe real time as well on a mobile phone?

Fast neural style transfer

The main idea behind fast neural style transfer is to build two models. One of them will do the image transformation in a feed-forward style from one image to another and the other is going to calculate a specific loss function between the style image and the content image in order to create visually pleasing style transferred images. It is nice, ain’t it? The loss-network has set weights that were trained to do some classification task in order to have meaningful representations of the images fed to it.

Where basically the transform network transforms the image to the desired style while the loss network just extracts features from all images to construct the target loss.

\[L_{content}^{\phi, j} (\hat{y}, y) = \frac{1}{C_j H_j W_j} || \phi(\hat{y}) - \phi{y} || ^{2}_{2}\]

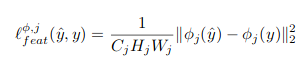
To make the content resamble the output image we simple take the Euclidian squared distance between the extracted feautres from the original image \(y\) and the transformed image \(\hat{y}\).

The style loss is a bit trickier. Since we want to keep the style of the style image and not its spatial features we drop spatial structure in a way that was introduced in the original neural style transfer paper the Gram matrix:

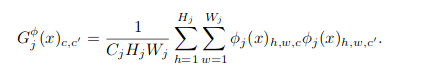
Where \(phi_j\) is a feature map extracted at some intermediate layer from the loss network. Given these Gram-metrices from several intermediate layers we can take the Forbenius-norm of the difference between the Gram-matrix of the style image through the loss net and the transformed image thourgh the loss net.

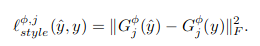
The total loss is just the sum of these losses with the appropriate hyperparameters which are not included in the paper and I couldn’t find it in the uploaded source code.

Here I include some steps that are not trivial, in order to make everything work I used Tensorflow:

• using tf.keras and importing the trained VGG16 network on should make adjustments due to the preprocessing step:
  • [0, 255] images are expected to the preprocessing and RGB is shifted to BGR for the VGG16 so during deprocessing one should take care of that
• due to the preprocessing the inference network’s output must be scaled to [0, 255] in order to provide valid images for the loss network, otherwise we would need to learn the preprocessing as well, which we do not intend to
• the inference network is a residual network which I found out from other open source implementations
• the loss functions also include total variation regularization which seems unimportant at this time for me

Useful code snippets

# Gram matrix calculation
# source : Neural style transfer  |  TensorFlow Core
def _gram_matrix(self, input_tensor):
        result = tf.linalg.einsum('bijc,bijd->bcd', input_tensor, input_tensor)
        input_shape = tf.shape(input_tensor)
        num_locations = tf.cast(
            input_shape[1] * input_shape[2] * input_shape[3], tf.float32)
        return result / num_locations

The Frobenius-norm is calculated for all the style layers:

def _style_loss(self, loss):
        STYLE_LAYERS = [
            'block1_conv1', 'block2_conv1', 'block3_conv1', 'block4_conv1',
            'block5_conv1'
        ]
        layer_weight = 1. / float(len(STYLE_LAYERS))
        style_final_loss = tf.cast(0., dtype=tf.float32)
        for loss_layer in STYLE_LAYERS:
            gram_style = self._gram_matrix(self.style_loss[loss_layer])
            bs, height, width, channels = self.style_loss[
                loss_layer].get_shape().as_list()
            gram_style = gram_style / (bs * height * width * channels)
            gram_reco = self._gram_matrix(loss[loss_layer])
            bs, height, width, channels = loss[loss_layer].get_shape().as_list(
            )
            gram_reco = gram_reco / (bs * height * width * channels)
            gram_diff = gram_reco - gram_style
            style_final_loss += layer_weight * tf.reduce_sum(
                tf.square(gram_diff) + tf.square(gram_diff) + 2. *
                tf.matmul(gram_diff, gram_diff, transpose_a=True))  # sqrd frob-norm
        return style_final_loss

Reference for the Forbenius-norm and the Frobenius inner product can be found on Wikipedia.

Conclusions

Setting the right hyperparameters is hard. I even had some difficulties with the size of the dataset since the original datasets contained 200’000 images or more and I had to use the CelebA face dataset in order to achive ‘results’. I’ll will post a methodological post about creating TFRecords in order to process data fast for Tensorflow models.

My implementation can be found on my GitHub.

Current status of the project:

The style image is the well-known self portrait of Van Gogh, while the results are faces from CelebA images:

It can be seen that something resambling to Van Gogh’s portrait happened to the images but it is nowhere near to original results. I must have some errors in my code that I am still debugging.

Future goals

It would be nice to see something like real time style transfer in the browser or on a mobile phone.

@Regards, Alex

Alex Olar

Christian, foodie, physicist, tech enthusiast

Tweet Share

comments powered by Disqus